- scritto da Giulia Azzini
- categoria Criteri Progettuali
Matematica e Architettura: dall’antichità fino ad oggi

Sin dall’antichità i più grandi architetti hanno basato le loro realizzazioni sulla matematica ed è proprio riferendosi a rigorosi modelli matematici e rigide proporzioni che hanno realizzato ciò che tutto il mondo oggi ammira, ovvero gli ordini architettonici. Declinati poi da ciascun architetto secondo canoni proporzionali personali, gli ordini architettonici sono esempio emblematico dell’applicazione di precise regole matematiche al mondo dell’architettura.
Matematica nell'architettura: le 8 configurazioni della casa origami
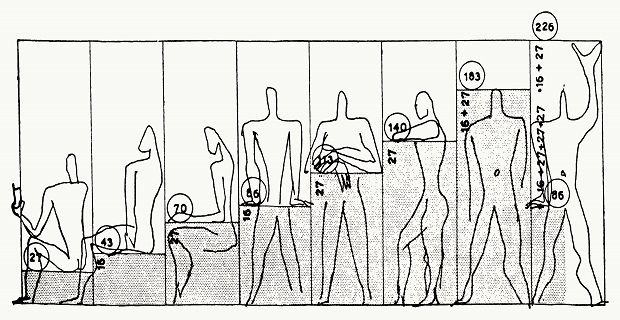
LA MATEMATICA DI LE CORBUSIER
Il connubio architettura-matematica ha trovato voce per esempio nell’opera di Le Corbusier. L’architetto studia il Modulor, il prototipo umano perfetto, proporzionato e matematicamente determinato. Sulla base delle sue misure vengono realizzati gli oggetti di arredo e gli ambienti stessi delle abitazioni. Le Corbusier utilizza anche nelle sue realizzazioni la sezione aurea.
Emblema di perfezione sin dal mondo ellenico classico, la sezione aurea viene ripresa e rivisitata da Le Corbusier in molte opere, una su tutte la candida Ville Savoy.
LA MATEMATICA IN ARCHITETTURA OGGI
Lunga la strada che matematica ed architettura hanno percorso insieme fino ad arrivare all’epoca moderna, nella quale la matematica e i suoi modelli diventano indispensabili per le realizzazione più ardite dei più famosi architetti del mondo.
Si pensi per esempio ai volumi frastagliati e scomposti di Eisenman, alle famosissime vele di Utzon, alle forme morbide di Gehry, all’astrattismo delle forme di Zaha Hadid, al rigore geometrico e strutturale di Calatrava e ad ogni altra grande espressione architettonica di oggi.
La realizzazione di una tale complessità di forme non sarebbe possibile senza l’utilizzo di sofisticati modelli matematici e programmi in grado di gestirli.
Se prendiamo ad esempio la Chiesa del Giubileo a Roma, progettata da Richard Meier impegando tra l'altro il cemento mangiasmog e autopulente, stiamo parlando di sezioni di calotte sferiche , mentre se consideriamo l’Oceanografic di Calatrava consideriamo persino un insieme di paraboloidi iperbolici. E ancora particolari ellissoidi sono visibili in molte opere di Jean Nouvel e Norman Foster.
LA MATEMATICA E L'URBANISTICA
Modelli matematici regolano quindi le forme della nostra architettura ma più in grande conformano le nostre città e le nostre maggiori metropoli.
Uno studio di alcuni scienziati della University of Colorado fa notare come per esempio il modello matematico dell’urban scaling sia valido oggi come nelle più antiche civiltà. Il modello è in grado di cogliere e descrivere come cambia la distribuzione di popolazione all’interno della città all’aumentare della stessa, sottolineando come non venga ampliato il territorio urbanizzato ma aumenti la densità demografica nelle zone centrali.
Questo è un esempio di modello descrittivo ovvero in grado di spiegare i fenomeni che accadono in una città. Altre tipologie di modelli sono in grado di prevedere mutamenti futuri delle città sotto diversi aspetti: sociali, economici, produttivi ma anche di gestione delle risorse. Le questioni essenziali per le quali oggi si studiano modelli sono per esempio come si distribuiscono le attività economiche di una città, come si muove il traffico al suo interno, come interagiscono tra loro diverse città, come e dove si sposta la popolazione residente.
La matematica quindi fornisce un grande aiuto nella pianificazione del nostro abitare e del nostro interagire all’interno delle grandi strutture urbane.
Fonti | Architetture dell'assurdo, John Silber, Architecture Now, Taschen


